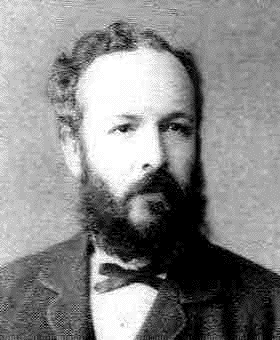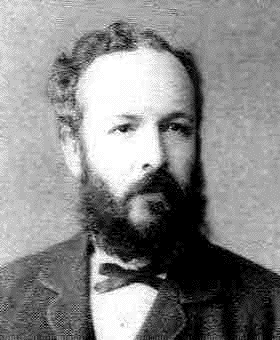Georg Ferdinand Ludwig
Philipp Cantor
1845 - 1918
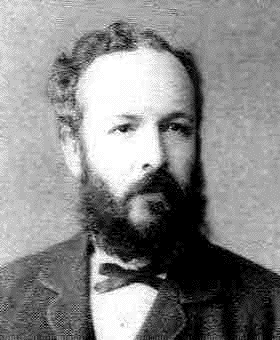
- Georg Cantor a fondé la théorie des ensembles, introduit
le concept de nombres infinis et fait progresser l'étude des séries
trigonométriques. Maître-assistant à l'université
de Zürich en 1862, il assistera à des conférences de
Weierstrass, Kummer et Kronecker à l'université de Berlin.
- Il obtient son doctorat en 1867 à Berlin et accepte un poste
à l'université de Halle en 1869, où il restera jusqu'en
1913. Ses premiers articles (1870-1872) montrent l'influence de l'enseignement
de Weierstrass. En 1872 il définit les nombres irrationnels dans
des termes de suites convergentes de nombres rationnels. L'année
suivante, il prouve que les nombres rationnels sont dénombrables,
i.e. qu'ils peuvent être placés dans une correspondance 1
à 1 avec les nombres naturels. Un nombre transcendant est un nombre
irrationnel qui n'est pas racine d'équation de polynôme avec
des coefficients entiers. Liouville établit en 1851 que les nombres
transcendants existent. Vingt ans plus tard Cantor montre que dans un certain
sens, presque tous les nombres sont transcendants. Le travail de Cantor
était attaqué par beaucoup de mathématiciens, dont
son propre professeur Kronecker. Cantor ne doutait jamais de son travail
malgré la découverte des paradoxes de théorie d'ensemble.
Il était soutenu par Dedekind, Weierstrass et Hilbert, Russell et
Zermelo. Cantor meurt dans une clinique psychiatrique en 1918.