Extraction de

 

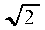
"Les nombres gouvernent le monde" pense Pythagore. Mais la diagonale d'un carré n'a aucune commune mesure avec son côté : l'extraction des racines est donc "illégitime". Aristote utilise la méthode du "raisonnement par l'absurde" : si le rapport de la diagonale au côté du carré est une fraction ordinaire, alors elle peut s'écrire sous la forme irréductible d'un numérateur sur un dénominateur :

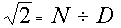
avec soit N impair, soit D impair, soit N et D impairs.

 

1) En élevant au carré, nous obtenons

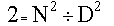
ou encore

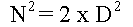
Cette expression (N au carré) est paire puisqu'elle est divisible par 2. Donc N est pair puisqu'un nombre impair au carré est impair.

 

2) si N est pair, il peut s'écrire sous la forme N = 2xM. Dans ce cas,

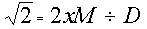
ou au carré

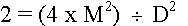
puis en divisant par 2

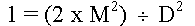
ou encore

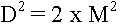
donc D est pair.

 

Les 1) et 2) sont en contradiction avec les conditions initiales qui postulent que N et D ne peuvent être pairs simultanément. Racine de 2 n'est donc pas égale à N/D (cette fraction ne peut pas exister).