Au début était la géométrie...

Dans l'antique Mésopotamie, les Sumériens avaient des notations différentes suivant qu'ils s'agissait d'objets qu'on peut compter un à un, comme des têtes de bétail, ou bien de mesures de volumes pour le liquide ou encore pour le grain, et ainsi de suite. Et puis, vers la fin du III° millénaire, les scribes sumériens ont inventé un système savant destiné à s'appliquer à tout ce qui se compte. C'est là qu'on voit se former ce concept de nombre abstrait dans la notation écrite. Ils unifient toutes les notations existantes sur la base soixante. Cela vient de l'un des systèmes métrologiques antérieurs dans lequel les multiplicateurs, pour passer d'une unité au groupement de l'échelon supérieur, étaient alternativement six et dix. Les Babyloniens hériteront ensuite de cette notation en base soixante, dont nous avons nous-même hérité dans notre décompte des heures, des minutes et des secondes.

Par contre, ni les Babyloniens, ni même les Egyptiens ne connaissaient les nombres rationnels. Les uns et les autres avaient certaines formes de fractions ; chez les Egyptiens, seules les fractions dont le numérateur est un sont connues. Avec leur système de base soixante, les Babyloniens écrivaient de la même façon ce que l'on appellerait aujourd'hui les chiffres après la virgule. Le clou vertical qui désignait l'unité pouvait désigner aussi bien soixante unités qu'un soixantième. Les fractions égyptiennes sont ce qu'on appelle quelque fois des quantièmes : face à un problème comme de partager une certaine ration entre plusieurs ouvriers d'un chantier et que le résultat ne tombe pas juste, les parties fractionnaires sont exprimées comme combinaison de fractions du type un quart, un huitième, un quatorzième, etc.

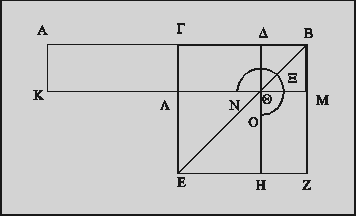Les Grecs ne possédaient pas non plus de nombres rationnels. Pour les mathématiciens grecs, les seuls nombres identifiés comme tels étaient les entiers. C'est l'école pythagoricienne, on ne sait pas exactement à quelle époque, au plus tard au V° siècle avant notre ère, qui a véritablement découvert l'irrationalité de certains rapports de grandeurs. En particulier la diagonale du carré a un rapport au côté du carré qui est irrationnel : cela signifie que ce rapport ne peut pas être égal au rapport de deux nombres entiers. Mais face au problème posé, ils ont inventé, non pas un nouveau type de nombres, mais une théorie des proportions entre grandeurs géométriques, complétement indépendante des nombres.

C'est ce qu'on trouve au livre V des Eléments d'Euclide : une théorie qui permet de manipuler des proportions entre des grandeurs géométriques. Mais jamais ces grandeurs ne sont conçues comme mesurées par des nombres. On ne peut donc pas dire que 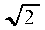(racine de 2) existe dans la mathématique grecque. Ce qui existe ce sont des grandeurs géométriques et des rapports entre grandeurs géométriques, qui ne sont pas forcément rationels.

Pi non plus n'est pas un nombre. Au livre XII des Eléments d'Euclide il y a une proposition qui dit que l'aire d'un cercle est proportionnelle au carré du rayon du cercle. On peut donc concevoir, dans le cadre de la géométrie grecque, le rapport entre l'aire du cercle et le carré du rayon. C'est ce que nous appellerions Pi, mais ce type de rapport n'est pas conçu comme un objet mathématique. Il s'agit de relations entre des grandeurs. Bien qu'Archimède en calcule une approximation, il n'y a pas de nombre 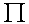(Pi) dans la mathématique grecque.

C'est sans doute en Grèce que naît la première réflexion sur l'identité du nombre, mais on ne sait pas très bien quand ni comment. Le premier texte mathématique que l'on possède, ces fameux Eléments d'Euclide, datent d'environ 300 avant notre ère, ce qui est déjà tardif par rapport à la Grèce classique. On ne connaît pas bien la genèse des conceptions qui y sont exprimées. Euclide définit un nombre comme une multiplicités d'unités, l'unité étant un concept primitif que l'on ne définit pas, qui est déjà là. Et en vertu de la théorie des proportions, la géométrie jouit d'une certaine prééminence sur le reste des mathématiques. Quand Euclide traite de la théorie des nombres, dans ses livres VII, VIII et IX il représente d'ailleurs les nombres à l'aide de segments de droite. Ce qui lui permet de raisonner sur des nombres non spécifiés, abstraits. Il ne dit même pas s'il s'agit de 2 ou de 3. Il dit : je considère un nombre et je le désigne par un segment de droite. Et à ces segments de droite, il applique des raisonnements géométriques. C'est donc la géométrie qui sert à la théorie des nombres.

Suite Géométrie et arithmétique