Les nouveaux nombres

A la fin du XIX° siècle, on peut considérer que le concept de nombre tel que nous l'entendons aujourd'hui est établi, bien qu'avec des nuances liées au statut qu'on attribue aux divers types de nombres. Il y a en particulier les nombres imaginaires et complexes, qui jouent un rôle fondamental dans toutes les parties des mathématiques. Les nombres imaginaires apparaissent pour la première fois dans un livre d'algèbre de Jérôme Cardan, un mathématicien de l'Italie du Nord, au XVI° siècle. Mais il n'en fait rien. Le premier texte où l'on voit vraiment à l'oeuvre ces nombres imaginaires est un peu ultérieur. Il est d'un autre italien, Bombelli, en 1572. Il s'agit simplement des racines carrées des nombres négatifs. Il y a une règle des signes connues depuis très longtemps qui dit que si l'on multiplie du plus par du plus, ou du moins par du moins, on obtient toujours du plus.

Donc un carré d'un nombre au sens ordinaire est forcément positif. Bombelli se place dans le cadre justement du développement arithmétique de la théorie des irrationnels, qui a son origine dans l'algèbre arabe. Il lui donne une extension plus grande. Il dit : j'ai découvert un nouveau type d'irrationnel, il donne les règles de calcul et montre que ces nombres sont utiles pour étudier l'équation du troisième degré. C'est une espèce de calcul formel, qui n'était pas du tout interprétable géométriquement. Par la suite, au XVII° siècle, Albert Girard en 1629 puis René Descartes ont énoncé qu'une équation algébrique a autant de racines, de solutions que son degré. Une équation du second degré a deux racines, une équation du troisième degré en a trois, etc. Dans sa Géométrie de 1637, appendice au célèbre Discours de la méthode, Descartes, comme Girard avant lui, explique qu'il y a autant de racines que de degrés mais que ces racines ne sont pas toujours réelles.

C'est là qu'il introduit le terme d'imaginaire (Girard disait "impossible"). Imaginaire, c'est-à-dire qu'on peut en imaginer autant qu'il y a de degrés. On peut les imaginer, c'est-à-dire les noter par des lettres, puisqu'on est dans le cadre d'une algèbre littérale, on peut les manipuler comme si c'étaient des nombres - bien qu'aux yeux de Girard et de Descartes ils n'en fussent pas vraiment. Ils y voyaient simplement des intermédiaires formels dans le calcul, très utiles parce qu'ils permettent de traiter d'une manière générale les problèmes d'algèbre. Faute de quoi, il fallait distinguer des quantités de cas. Albert Girard le dit explicitement : on introduit cela pour avoir des règles générales. Au XVIII° siècle, on a commencé par démontrer que ces imaginaires - on ne savait pas trop ce que c'était - étaient utilisables pour le calcul intégral. Mais du coup, on ne pouvait plus se contenter de dire qu'il ne s'agissait que d'objets formels, parce qu'on avait besoin d'écrire, par exemple, le logarithme d'un imaginaire. Il fallait essayer d'interpréter ce que cela pouvait bien être. Dans la pratique, le nombre imaginaire intervenait toujours dans un couple de nombres réels. C'est ce couple qu'on appelle nombre complexe. Il comprend une quantité réelle disons p, plus une autre quantité réelle, q, multipliée par  (racine de -1). La seule intervention de l'"impossibilité", c'est l'introduction de . Ce sont les nombres complexes qui ont permis à d'Alembert, en 1746, d'engager la démonstration de ce que l'on appelle le théorème fondamental de l'algèbre. Il précise l'énoncé par Descartes, selon lequel une équation a autant de racines que de degrés, en montrant que les racines imaginaires introduites par le philosophe-mathématicien sont toutes de la forme : p + q . La démonstration complète est due à Gauss (1799).

Les nombres complexes sont indispensables entre autres pour étudier les nombres entiers. Le cas typique c'est le dernier théorème de Fermat, un contemporain de Pascal. Ce théorème dit que lorsque n est un entier strictement supérieur à 2, il n'existe pas d'entiers positifs non nuls a, b, c, vérifiant l'équation 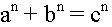. Le cas le plus simple est qu'une somme de deux cubes ne peut pas être un cube. Or, déjà, ce cas exige l'intervention de nombres complexes. La somme de deux cubes peut être décomposée en facteurs. 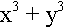 est divisible par x + y. Le quotient est 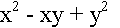. Cette formule peut encore être factorisée, mais il faut utiliser des nombres complexes, car cela met en jeu une équation du second degré qui n'a pas de racine réelle. On voit apparaître les trois racines cubiques de l'unité. La démonstration a été fournie par Euler au XVIII° siècle.

Il est également nécessaire d'introduire des nombres complexes pour étudier la suite des nombres premiers. Encore aujourd'hui l'un des problèmes centraux des mathématiques est de savoir comment sont distribués les nombres premiers dans la suite des entiers. Ils apparaissent de manière inattendue. On sait qu'ils se raréfient à mesure qu'on avance dans la suite des entiers, mais on ne parvient pas à déterminer la règle qui préside à leur apparition. Le premier théorème qui ait donné une information sur la manière dont ils se raréfient progressivement n'a été démontré qu'il y a un siècle, en 1896, indépendamment par le Français Hadamard et le Belge La Vallée-Poussin. Pour y parvenir, il leur fallut utiliser les propriétés analytiques d'une certaine fonction, qu'on appelle la fonction zeta de Riemann, qui en fait avait déjà été introduite par Euler au XVIII° siècle, et qui fait appel aux nombres complexes.

Suite Sur la réalité du nombre